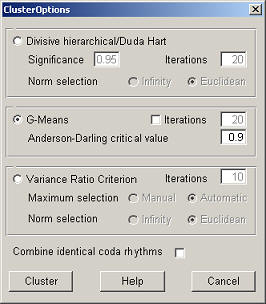

Three different clustering algorithms are available, divisive hierarchical, g-means and the variance ratio criterion. There is no best performing algorithm, the one that should be used depends on the data set. In short, the divisive hierarchical algorithm (DH) clusters the codas in the space spanned by the inter-pulse intervals searching for clusters with a n-dimensional spherical normal distribution. It continues clustering until the resulting partitioning is no longer improving according to the Duda Hart ratio criterion. The g-means (GM) algorithm also performs the clustering in the high dimensional inter-pulse interval space but projects the resulting clusters onto a single dimension in the direction of their principal components and then accepts a cluster if it follows a normal distribution according to the Anderson-Darling statistic. It stops clustering as soon as it finds an acceptable model and does not continue in an attempt to maximize a criterion. Apart from the criterion, another difference between DH and GM is that DH always tries to split clusters in two to improve the model, whereas GM reclusters the complete dataset of not-accepted clusters with an increased value of k for k-means. The variance ratio criterion (VR) calculates the ratio of the between- and within cluster sum-of-squares for a number of models (from 2 up to 10 clusters) and selects the optimal clustering, this algorithm is not specifically biased towards normal distributions.
Divisive hierarchical/Duda Hart
Significance
This is the p-percent significance level used for the criterion suggested by Duda-Hart, see the description of the algorithm. (Note that it is not a percentage here, ie. use 0.95 for 95%).
Iterations
The algorithm makes use of k-means and to prevent random outcomes the clustering should be performed a number of times.
Norm selection
The distance function used with k-means can be set to the infinity or Euclidean norm.
G-Means
Anderson-Darling critical value
This is the critical value used for the Anderson-Darling test. A complete description of the followed clustering algorithm can be read here.
Iterations
When enabled the k-means algorithm is run multiple times with random initializations. If not enabled k-means is used with a deterministic initialization where the starting centers are selected at a maximum distance from each other.
Variance Ratio Criterion
Iterations
The algorithm makes use of k-means and to prevent random outcomes the clustering should be performed a number of times.
Maximum Selection
The first local maximum can be selected automatically or manually. If automatic selection is chosen then the number of clusters should be checked for correctness in the coda view window. In the case of manual selection the user can select one of the ratios from a plot drawn by the program (the number of clusters must be chosen between two and ten).
Combine identical coda rhythms
As explained in the naming protocol section, the names for the coda clusters are related to a number of different rhythmic patterns and it is possible that several clusters follow the same rhythm (this can especially be the case with 3-pulse codas which generally do not cluster well using normal distributions as models). Checking this option will combine clusters with similar rhythms into one.
Cluster
Continues clustering with the given parameters.
Help
Opens this help page. The help page is opened in a new window because the Cluster Options window is set modal and it seems that this does not permit interaction with an existing help window.
Cancel
Cancels clustering and returns to the main window.
Click here to go to the main index.